Các dạng bài bác tập Đại số cùng Giải tích lớp 11 chọn lọc có lời giải
Với các dạng bài xích tập Đại số và Giải tích lớp 11 tinh lọc có giải thuật Toán lớp 11 tổng hòa hợp trên 50 dạng bài bác tập, trên 1000 bài xích tập trắc nghiệm gồm lời giải chi tiết với đầy đủ phương thức giải, lấy ví dụ minh họa để giúp đỡ học sinh ôn tập, biết cách làm dạng bài tập Đại số với Giải tích từ kia đạt điểm cao trong bài bác thi môn Toán lớp 11.
Bạn đang xem: Các dạng toán lớp 11

Chuyên đề: Hàm số lượng giác - phương trình lượng giác
Chủ đề: Hàm số lượng giác
Chủ đề: Phương trình lượng giác
Bài tập trắc nghiệm
Chuyên đề: Tổ hợp - Xác suất
Chủ đề: Tổ hợp
Chủ đề: Xác suất
Chuyên đề: Dãy số - Cấp số cộng và cấp số nhân
Các dạng bài xích tập chương Dãy số - Cấp số cộng, cấp số nhân
Phương pháp quy nạp toán học
Dãy số
Cấp số cộng
Cấp số nhân
Bài tập trắc nghiệm
Chuyên đề: Giới hạn
Chủ đề: giới hạn của hàng số
Chủ đề: số lượng giới hạn của hàm số
Chủ đề: Hàm số liên tục
Chuyên đề: Đạo hàm
Các dạng bài tập chương Đạo hàm
Cách tính Đạo hàm
Viết phương trình Tiếp tuyến
Vi phân, đạo hàm v.i.p & ý nghĩa của đạo hàm
Cách tra cứu Tập xác định, tập cực hiếm của hàm số lượng giác
A. Phương pháp giải và Ví dụ
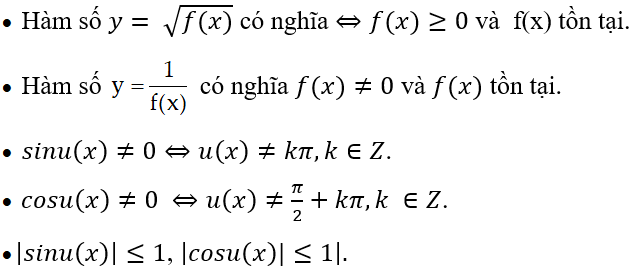
Ví dụ minh họa
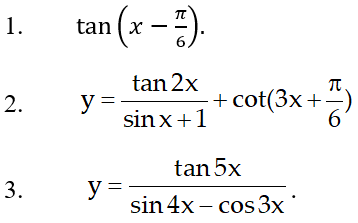
Đáp án và hướng dẫn giải
1.
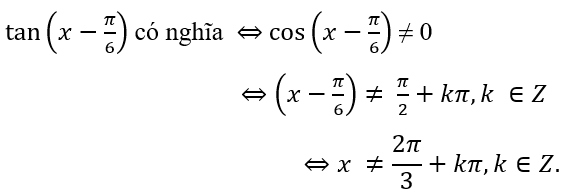
Vậy tập xác định của hàm số bên trên là
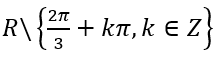
2.
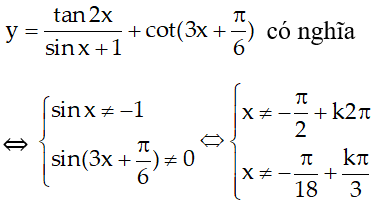
Vậy tập khẳng định của hàm số trên là
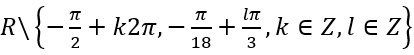
3.
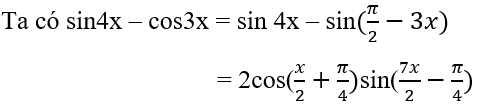
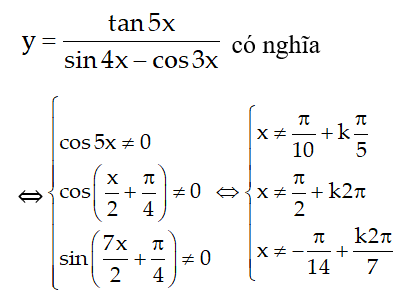
Vậy tập khẳng định của hàm số bên trên là
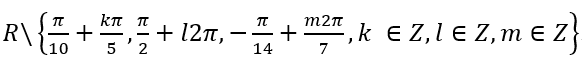
B. Bài bác tập vận dụng
Bài 1: tìm kiếm tập xác định của những hàm số sau:
a) tan(2x - π/4) b) cot (2x-2)
Lời giải:
a.
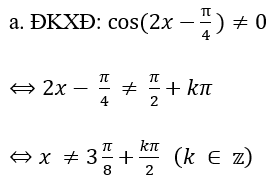
b. ĐKXĐ: sin(2x-2) ≠ 0 ⇔ 2x-2 ≠ kπ ⇔ x ≠ kπ/2 + 1 (k ∈ z)
Bài 2: tra cứu tập khẳng định và tập giá trị của các hàm số sau:

Lời giải:
a. ĐKXĐ: x ≠1
Tập giá trị: D= <-1 ,1>
b. ĐKXĐ: cosx ≥ 0
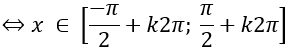
Tập giá trị: D= <0,1>
Bài 3: tra cứu tập giá chỉ trị của các hàm số sau:

Lời giải:
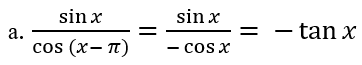
⇒ tập giá chỉ trị∶ D= R
b. Ta có:
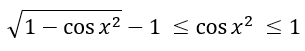
⇒ 0 ≤ 1-cosx2 ≤ 2 ⇒ tập quý hiếm = <0,√2>
Bài 4: tìm kiếm tập xác minh của những hàm số sau:

Lời giải:
a. làm giống VD ý 3
b.
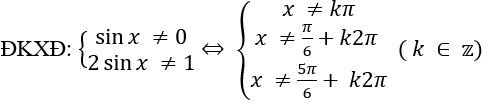
Bài 5: tìm tập xác định của các hàm số sau:

Lời giải:
a. ĐKXĐ:
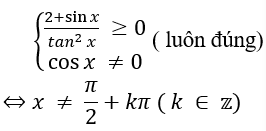
b. ĐKXĐ:
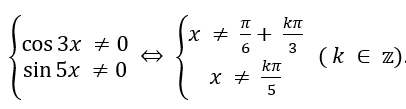
Cách xét Tính chẵn, lẻ với chu kì của hàm con số giác
A. Cách thức giải & Ví dụ
a. Tính tuần hoàn cùng chu kì:
Định nghĩa: Hàm số y = f(x) bao gồm tập khẳng định được call là hàm số tuần hoàn, nếu tồn tại một trong những T≠0 làm thế nào cho với gần như x ∈ D ta có:
♦(x- T) ∈ D cùng (x + T) ∈ D
♦f (x + T) = f(x).
Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó. Tín đồ ta chứng minh được rằng hàm số y = sinx tuần hoàn với chu kì T = 2 π ; hàm số y = cosx tuần hoàn với chu kì T = 2 π; hàm số y = tanx tuần trả với chu kì T = π; hàm số y = cotx tuần trả với chu kì T = π
Chú ý:
Hàm số y = sin(ax + b) tuần trả với chu kì T =
Hàm số y = cos(ax + b) tuần hoàn với chu kì T =
Hàm số y = tan(ax + b) tuần trả với chu kì T =
Hàm số y = cot(ax + b) tuần hoàn với chu kì T =
Hàm số y = f1(x) tuần hoàn với chu kì T1 và hàm số y = f2(x) tuần trả với chu kì T2 thì hàm số y = f1(x) ± f2(x) tuần trả với chu kì T0 là bội chung nhỏ dại nhất của T1 cùng T2 .
b. Hàm số chẵn, lẻ:
Định nghĩa:
Hàm số y = f(x) có tập xác định là D được gọi là hàm số chẵn nếu:
♦x ∈ D cùng – x ∈ D.
♦f(x) = f(-x).
Hàm số y = f(x) tất cả tập xác minh là D được hotline là hàm số lẻ nếu:
♦x ∈ D cùng – x ∈ D.
♦f(x) = - f(-x).
Ví dụ minh họa
Bài 1: Xét tính tuần hoàn với tìm chu kì cơ sở của những hàm số sau:
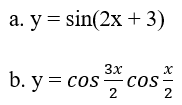
Hướng dẫn giải
a. Hàm số đã mang lại tuần trả với chu kì T = 2π/2 = π.
b.
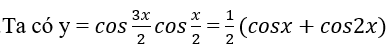
Ta tất cả hàm số y = cosx tuần trả với chu kì T = 2 π , hàm số y = cos2x tuần trả với chu kì T = π. Vậy hàm số đã mang lại tuần hoàn với chu kì T = 2 π .
Bài 2: Xét tính tuần hoàn cùng tìm chu kì cơ sở của những hàm số sau: y = cosx + cos√3x.
Hướng dẫn giải
Giả sử hàm số đã đến tuần hoàn với chu kì T ≠ 0. Lúc ấy ta có:
cos(x + T) + cos<√3(x +T)> = cosx + cos√3x.
Cho x = 0. Ta có: cosT + cos√3T = 2. Bởi cosx ≤ 1 với tất cả x yêu cầu ta có:
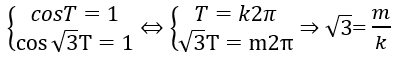
mà m, k ∈ Z (vô lý). Vậy hàm số đã đến không tuần hoàn.
Bài 3: Xét tính chẵn lẻ của các hàm số sau:
a. y = sinx.
b. y = cos(2x).
c. y = tanx + cos(2x + 1).
Hướng dẫn giải
a. Tập khẳng định D = R. Lấy x ∈ D thì – x ∈ D. Ta có: sin (-x) = -sinx. Vậy hàm số đã chỉ ra rằng hàm số lẻ.
b. Tập xác minh D = R. Lấy x ∈ D thì – x ∈ D. Ta có: cos(-2x) = cos(2x). Vậy hàm số đã cho rằng hàm số chẵn.
c.
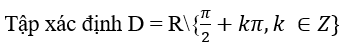
Lấy x ∈ D thì – x ∈ D. Ta có:
tan(-x) + cos(-2x + 1) = -tanx + cos(-2x + 1).
Vậy hàm số đã cho không chẵn, ko lẻ.
B. Bài tập vận dụng
Bài 1: Xét tính tuần hoàn cùng tìm chu kì cơ sở của các hàm số sau:
a) y = cos(-2x +4)
b) y = tan(7x + 5)
Lời giải:
a) Hàm số đã mang đến làm hàm tuần trả với chu kì T = 2π/2 = π
b) Hàm số đã cho làm hàm tuần hoàn với chu kì T =π /7.
Bài 2: Xét tính tuần hoàn và tìm chu kì các đại lý của hàm số sau: y = sinx + sin3x
Lời giải:
Ta gồm y = sinx là hàm tuần trả với chu kì T = 2 π cùng hàm số y = sin3x là hàm tuần trả với chu kì T = (2 π)/3. Vậy hàm số đã cho là hàm tuần trả với chu kì T = 2 π .
Bài 3: Xét tính tuần hoàn với tìm chu kì cơ sở của các hàm số sau: y = cosx + 2sin5x
Lời giải:
Làm giống như bài 2 và sử dụng chăm chú phần tính tuần hoàn với chu kì, ta có hàm số đã cho là hàm tuần hoàn với chu kì T = 2 π .
Bài 4: Xét tính chẵn, lẻ của các hàm số sau:
a) y = cosx + cos2x
b) y = tanx + cotx.
Lời giải:
a) Ta có tập xác minh của hàm số là D = R.
cos(-x) + cos(-2x) = cosx + cos2x. Vậy hàm số đã cho là hàm số chẵn.
b) Ta có tập khẳng định của hàm số là D = Rk π/2, k ∈ Z.
tan(-x) + cot(-x) = - tanx – cotx. Vậy hàm số đã chỉ ra rằng hàm số lẻ.
Bài 5: Xét tính chẵn, lẻ của các hàm số sau:
a) y = cosx + sinx.
b) y = sin2x + cot100x
Lời giải:
a) Ta bao gồm tập xác minh của hàm số là D = R.
Xem thêm: Giá Kính Chắn Gió Xe Innova, Và Các Công Đoạn Thay Thế Kinh Chắn Gió
sin (-x) + cos(-x) = - sinx + cosx. Vậy hàm số đã chỉ ra rằng hàm không chẵn, không lẻ.